第9話 長方形で容器づくり（3）
--お父さんも帰ってくる。かずきは早速報告を始める。
お父さん「そうか。すごいな，小田さんって子は。だから言ったろう，算数のよさは物事をすっきりと考えられることだって。ところで，おい，まどかはどうしたんだ」
お母さん「何だか『調べごとの途中（とちゅう）だから，先に夕食を食べてて』と言ったきり，部屋から出てこないのよ」
かずき「昨日のお母さんの問題を解きつくすんだって」
お父さん「へぇー，さすが俺（おれ）に似て粘り強いな，まどかは」
--お父さんが夕食を始める。
まどか「わかったわ。またまたカンペキよ。いい？みんな！」
--まどかは3人を前にして話し出した。
まどか「昨日のお母さんの問題で実験した結果と，今日のかずきの学校での小田さんの考えから，長方形から筒（つつ）をつくるときには，長い辺の方を底にした方がたくさん水の入る容器がつくれることがわかったと思うの」
お母さん「そうね。どちらの結果もそうなったものね」
まどか「でもね，『いつでも必ずそのことがいえるかどうか』は，実験や特定の数値だけでの説明では不十分だって思ったんだ」
かずき「何で？だって，もう2つも考えが出たんだからいいじゃん！」
まどか「かずきは，もし，縦の長さが30cm，横の長さが40cmの長方形でやっても，まちがいなく長い方の辺を下にしたほうが体積が大きくなる，って言える？結果が逆にならないって保証できる？」
かずき「うーん，そう言われると...」
まどか「そこで，そんなときは数学の先生が「文字に置きかえて考えてみればいい」って言ったのを思い出したのよ」
--まどかの説明に聞き入る3人。
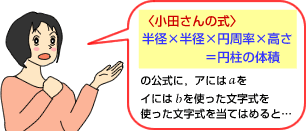
まどか「そこで，小田さんの考えで，長い方の辺の長さの60（cm）をa（cm）に，短い方の辺の長さの30（cm）をb（cm）に置きかえてみたの（図5）。かずきはまだ，勉強してないかもしれないけど，中学では円周率をπ（パイ）で表すんだ。でも，3や3.14と同じことだと思って聞いてて。」
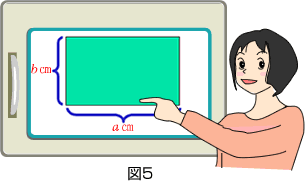
まどか「まず，ア・イの底面の半径を出してみるね。半径が分かれば，昨日の小田さんの考えを応用して体積を求めることができるはず！数学の時間に勉強した,
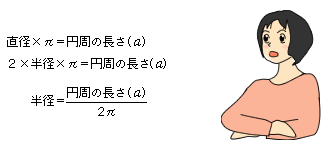
という式に，ア・イそれぞれの底面の円周の長さをあてはめると...」（図6）
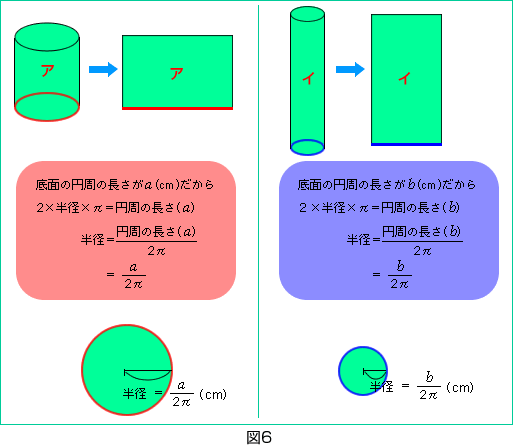
まどか「アの半径は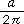
，イの半径は
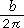って文字で表すことができたんだ。そうすると，容器の体積も，小田さんの式の半径を表す10（cm）のところに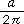（cm）を，5cmのところを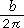（cm）に置き換えて求めることができるの。すると，文字で体積が表せる！」（図7）
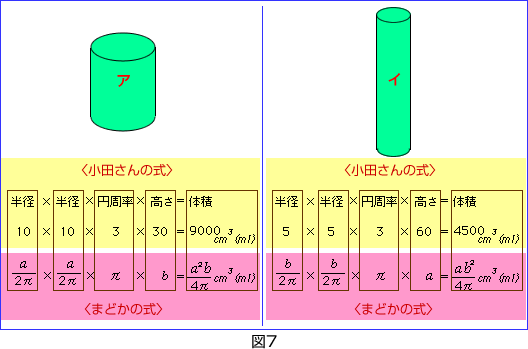
お母さん「すごいわね，まどか。何だか難しい式になったわね。私はついていけないわ」
お父さん「でも，何だか似ているね」
まどか「そうなのよ。これだけでは，アとイのどちらが大きいのかがよくわからないでしょ。でも，よく見ると，アもイも分母は4πで同じ。分子はaと bが一つずつがあるでしょ」
かずき「同じものがあると，何なの？」
お父さん「とっちゃっても関係ない，ってことかな。ほら，つりあっているシーソーの両方から同じ重さの人がいなくなっても，つりあいは変わらないだろう」
まどか「そうなのよ，お父さん。つまり，残ったのはアはaだけ，イはbだけなの。つまり，アとイの容器の体積の関係は，もとの長方形の長い方の辺の長さと短い方の辺の長さの関係になるのよ！」
お父さん
お母さん「お見事！」
かずき「何だかわかんないけど，やっぱり長い方を下にした方が必ず多く入れることができるんだね」
お父さん「そういうことだな。まどかは，それがまちがいないってことを証明してくれたんだ。でも，なぜそこまで考える気になったんだい」
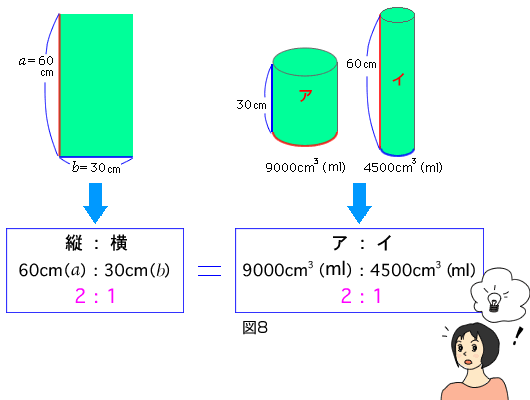
まどか「かずきが持ってきてくれた小田さんの考えで使った長方形の縦横の比2：1が，そのまま体積比の2：1になっていたのよ。偶然かなって思って，3：1の比の長方形でやってみたら，やっぱり体積も3：1になったの。これは，絶対関係があるって思って」 （図8）
お父さん「うーん，まどかはやっぱりお父さんの子だな」
かずき「ボクもお父さんの子だよぉ...」
--一同大笑い...。
